External Ballistics
Video Library
From Barrel to Target
External ballistics deals with the performance of Hornady bullets from the moment they exit the barrel until the moment they arrive at the target. We are not concerned with internal ballistics, the province of the firearms engineer or powder chemist, nor with terminal ballistics, the province of the forensic pathologist or other scientific specialists.
Terminal ballistics is a very important concern to the military, to police, and to hunters. While there is no way to model the terminal behavior of all projectiles in all media at all velocities, we'll mention the subject briefly in the section entitled An Aside on Energy. For now, we'll focus on exterior ballistics.
A trajectory is a description of the flight path of a projectile relative to some known and fixed points. Trajectories for BBs, field artillery projectiles, naval gun shells, mortar rounds, and small arms bullets are all parabolic in shape. In a barrel or mortar, the motion of a projectile is both directed and entirely determined by the pressures of the gasses behind it. But once the projectile leaves a barrel, two other forces begin to influence its flight. The first is air resistance. The second is gravity. Whatever its angle of departure and whatever its muzzle velocity, a shell or bullet will lose velocity from air resistance and lose height because of gravity. The parabolic shape of a trajectory is the result.
Narrowing our discussion to bullets only, we can provide illustrations of the parabolic curve of a trajectory and concepts related to it. In Figure A (exaggerated for purposes of illustration) we show a muzzle (left) and target (right) assumed to be horizontal on the same baseline (for practical purposes the baseline is equivalent to the line of sight). The firearm's barrel is elevated. The axis of the bore becomes the line of departure for a bullet leaving its muzzle. Gravity and air resistance come into play so fast that the bullet departure line is tangent to the trajectory only at the muzzle.
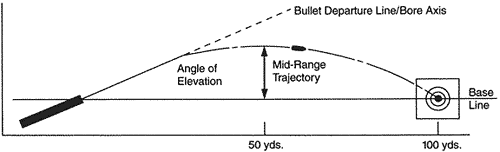
Figure A
The trajectory immediately begins to drop below the bore axis. The angle of departure (for small arms generally very small) is formed by the intersection of the line of departure and the baseline. The midrange trajectory is the bullet's height above the base line halfway between the muzzle and the point of impact (here, the target).
Figure B uses the same firearm, bullet, and muzzle velocity to compare two different trajectories (the barrel is represented for simplicity in only one position). The difference between trajectories results from different angles of departure required to zero the firearm (change its point of impact) at two ranges; 100 yards and 200 yards. Trajectories fall below the baseline (line of sight) in Figure B at zeros of 100 and 200 yards respectively. Bullet trajectories beyond their point of impact are described in terms of inches of drop.
While it makes sense to calculate trajectories for naval shells in terms of angles of departure and while one could do this for small arms trajectories as well, the shooter's primary reference in the field is the line of sight.
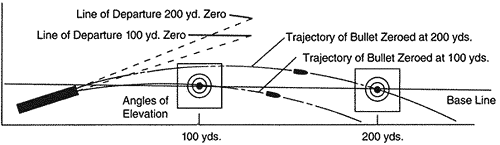
Figure B
The Ballistic Coefficient
Before discussing this topic in more detail, let's dispel some myths surrounding it. Whatever you may have heard before, these are the facts:
- There is no such thing as an absolute and invariable ballistic coefficient (B. C.)
- Ballistic coefficients are only one factor in bullet selection for different kinds of shooting.
- A ballistic coefficient can change with reference to (1) altitude, (2) temperature, (3) atmospheric pressure, and (4) relative humidity.
- Ballistic coefficients are measures of a bullet's relative efficiency.
- Ballistic coefficients are not measures of a bullet's "goodness."
- Higher B.C.s do not necessarily make a bullet "better."
- Lower B.C.s do not necessarily make a bullet "worse."
A ballistic coefficient is the measure of a bullet's relative ability to overcome air resistance. Each bullet can be assigned a numerical value expressing this efficiency. The basis of this value is a ratio comparing the performance characteristics of a particular bullet against the known trajectory characteristics of a standard projectile. The ratio compares the drag of a bullet (loss of velocity caused by air resistance encountered in flight) to the drag of the standard projectile. Expressed as a formula,

Observe that the ballistic coefficients in this book are, with only one exception, less than unity [1.0], indicating that these test projectiles - bullets for small arms - encountered more resistance than the standard. The single exception in the entire line of Hornady Bullets is our 50 Caliber (.510" diameter) 750 grain AMAX Ultra High Coefficient. Its ballistic coefficient is 1.050.
The standard projectile on which all Hornady Bullets were compared was the G1 Model, based on work begun in France and refined at the U. S. Army Ballistic Research Laboratories, Aberdeen Proving Ground, Maryland. Ballistic coefficients for all Hornady Bullets were determined by computer calculations using data from test firing research performed in our 200 yard underground test range. Our ELD-X® and ELD® Match bullets are measured with Doppler radar at extended distances.
Ballistic coefficient calculations combine both shape and sectional density factors. As a practical matter, most shooters understand that bullets with a pointed shape more easily retain their velocity than round nose or flat point bullets. This can be directly observed in the amount of drop bullets of the same weight but different shapes produce at the same target range. Expressed another way, round nose and pointed bullets will require different sight adjustments to attain the same zero over the same range. If more streamlined bullets maintain their velocity better, heavier streamlined bullets of the same shape will outperform lighter bullets at the same muzzle velocity.
The following examples quickly demonstrate the importance of shape to velocity retention and flat trajectory. We have chosen to compare in this example two bullets of identical caliber, weight, and sectional density fired at identical 3000 fps muzzle velocities. Shape is the only variable in this example; all other factors have been held constant. Observe the marked difference in bullet behavior over the ranges shown. The round nose bullet sheds its initial velocity faster than the spire point. Because energy is the product of mass x velocity squared, the round nose bullet's more rapid velocity loss produces an even faster loss of energy. Most dramatically, as the less efficient round nose shape loses its velocity, the effects of gravity show up in terms of greater bullet drop relative to the spire point bullet.
30 CAL. (.308" DIA.) 180 Grain Spire Point
Sectional Density: 0.271
Ballistic Coefficient: 0.425
| Range (YDS) | Velocity (FPS) | Energy (FT-LB) | 100 YD ZERO |
| Muzzle | 3000 | 3597 | -1.5" |
| 50 | 2887 | 3331 | -0.2" |
| 100 | 2777 | 3082 | 0.0" |
| 200 | 2565 | 2629 | -3.0" |
| 300 | 2362 | 2230 | -11.3" |
| 400 | 2169 | 1880 | -25.9" |
| 500 | 1985 | 1574 | -47.8" |
30 CAL. (.308" DIA.) 180 Grain Round Nose
Sectional Density: 0.271
Ballistic Coefficient: 0.241
| Range (YDS) | Velocity (FPS) | Energy (ft-lb) | 100 YD Zero |
| Muzzle | 3000 | 3597 | -1.5" |
| 50 | 2803 | 3139 | -0.2" |
| 100 | 2614 | 2731 | 0.0" |
| 200 | 2259 | 2040 | -3.6" |
| 300 | 1933 | 1493 | -14.1" |
| 400 | 1639 | 1073 | -34.0" |
| 500 | 1385 | 767 | -67.0" |
Does this comparison argue entirely against using round nose bullets? By no means; over the 100 to 200 yard ranges typical of a great deal of hunting, the round nose holds its own. Moreover, many who hunt with them regard them as utterly reliable over their intended distances. Confidence counts more than a lower ballistic coefficient to these folk.
Correction Factors
Ballistic coefficients are calculated not only with reference to a standard projectile but with reference to standard test conditions as well. All ballistic coefficients and ballistic tables in this book have been adjusted to standard conditions. These are standard conditions for the Aberdeen test site.
- Altitude: Sea level
- Temperature: 59° Fahrenheit
- Atmospheric pressure: 29.53" of Hg
- Relative humidity: 78%
What happens when the conditions are not standard? These four test examples will demonstrate changes in a calculated ballistic coefficient resulting from varying different test factors in turn.
Test #1: Standard Conditions
Altitude: Sea Level
Temperature: 59° F
Barometric Pressure: 29.53"
Relative Humidity: 78%
| Range (YDS) | Velocity (FPS) | Trajectory 100 YD Zero |
| Muzzle | 2900 | -1.5" |
| 100 | 2627 | 0.0" |
| 200 | 2371 | -3.6" |
| 300 | 2129 | -13.3" |
| 400 | 1901 | -30.8" |
| 500 | 1690 | -57.9" |
Results: Calculated ballistic coefficient is .338
Test #2: Higher Temperature
Altitude: Sea Level
Temperature: 89° F
Barometric Pressure: 29.53"
Relative Humidity: 78%
| Range (YDS) | Velocity (FPS) | Trajectory 100 YD Zero |
| Muzzle | 2900 | -1.5" |
| 100 | 2640 | 0.0" |
| 200 | 2395 | -3.5" |
| 300 | 2162 | -13.1" |
| 400 | 1943 | -30.1" |
| 500 | 1739 | -56.4" |
Results: Due to less dense air (warmer temperatures) the calculated B.C. is .355.
Test #3: Higher Barometric Pressure
Altitude: Sea Level
Temperature: 59° F
Barometric Pressure: 31.00"
Relative Humidity: 78%
| Range (YDS) | Velocity (FPS) | Trajectory 100 YD Zero |
| Muzzle | 2900 | -1.5" |
| 100 | 2614 | 0.0" |
| 200 | 2346 | -3.6" |
| 300 | 2094 | -13.6" |
| 400 | 1858 | -31.5" |
| 500 | 1641 | -59.5" |
Results: Due to denser air (higher barometric pressure) the calculated B.C. is .322.
Test #4: Higher Altitude
Altitude: Sea Level
Temperature: 29° F
Barometric Pressure: 21.00"
Relative Humidity: 78%
| Range (YDS) | Velocity (FPS) | Trajectory 100 YD Zero |
| Muzzle | 2900 | -1.5" |
| 100 | 2693 | 0.0" |
| 200 | 2495 | -3.3" |
| 300 | 2306 | -12.2" |
| 400 | 2124 | -27.6" |
| 500 | 1952 | -50.8" |
Results: Due to less dense air (higher altitude) the calculated B.C. is .448.
The .338 calculated ballistic coefficient has ranged from .322 to .448 as conditions have varied. Common sense suggests that a bullet might perform better in higher temperatures (less dense air), at lower barometric pressures (less air pressure), and at higher altitudes (much lighter air). When there is less air to resist a bullet's flight, it will become more efficient - and conversely. How can you account for significantly non-standard conditions in preparing, say, for a major hunt? Assuming that you know the temperature, barometric pressure, and ballistic coefficient of the bullet you will be shooting in non-standard conditions, you can calculate the apparent ballistic coefficient of the bullet and otherwise find the trajectory for your non-standard condition site.
The drag on a bullet is largely produced by the density of the air through which it travels. The first conversion factor to correct for changes in air density is the ratio of:

which is used as a multiplier in the correction calculation. The correction factor for temperature is another ratio, but with a twist:

The 459.4° addition to the site temperature and standard temperature is to place both in the absolute Rankine Scale. (Absolute zero is -459.4° Fahrenheit or 0° Rankine.) The resulting ratio is also a multiplier in the correction process.
Corrections can be made as well for relative humidity, but the correction process is tedious and the precision gained is negligible. At any rate, while we've seen barometers in camp and thermometers on the trail, we can't recall seeing hunters lugging hygrometers. Besides, we have already captured the primary factors requiring adjustment.
Assume that we encounter the following conditions on a hunt. The temperature is a chilly 29° Fahrenheit, the barometric pressure 21.00"Hg., and the relative humidity 85%. Think about this a minute and it seems we're on a mountain hunt in some very raw conditions. Relative humidity is very close to the standard 78%, so we'll not worry about adjustments there. But the temperature and atmospheric pressure are far from standard. What effect will they have on the ammunition we've loaded with a standard condition ballistic coefficient of .338?
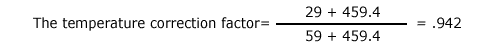

The Apparent Ballistic Coefficient=Temperature correction factor x Barometric pressure correction factor x Present ballistic coefficient=.942 x 1.406 x .338=.448.
As a practical matter, the lower temperature alone would reduce the apparent ballistic coefficient, but in combination with the low barometric pressure correction the overall result will be flatter trajectories for the ammunition brought on this hunt.
Shooters who go from low altitudes to high altitudes or vice versa should bring along enough ammunition to sight in their firearms at the new location. The flat trajectories obtained with reloads in Fort Collins, Colorado may not be so flat on a hunt in the woods of Maine. Aiming higher over common ranges is the answer here. Conversely, taking tested loads from Mobile, Alabama to the mountains of British Columbia may require aiming lower than one might have back home.
For ranges up to and including 300 yards, ballistic coefficient corrections may not, practically speaking, be required. Steadiness of the shooting position and the aiming skills of the shooter may account for more difference between planned and actual trajectory than correction factors might require. If actual shooting conditions are going to be dramatically different from those at home, it's sound advice to take enough ammunition to re-zero your firearm at the shooting site.
An Aside on Energy
Over the years many writers have spent considerable time pursuing the concept of bullet performance. In match competition or target shooting, performance standards are simple and direct. Bullets for target shooting should be highly efficient (streamlined, possessing a high ballistic coefficient) in order to shoot as flat as possible and buck the effects of wind drift. Efficiency counts for naught, however, if these bullets are not accurate as well - made so carefully and precisely that they will routinely yield sub-minute-of-angle performance on targets.
Performance for hunting bullets, however, is a far more complex matter. Some have contended that you must expect to find your splendidly mushroomed bullet under the game animal's hide opposite the entry hole. Shame on you if it doesn't weigh used 95% of what it weighed new. Others have said it's fine if the bullet enters and exits its target as long as it does deadly damage on its way. Pragmatists are pleased with bullets that strike where aimed and drop and kill the game immediately. They are hunters, they argue, not forensic pathologists.
Is performance a matter of opinion only? Of conjecture? A subject like religion and politics on which there will always be disagreement?
The experienced hunter knows that he will never be presented only with perfect shots under ideal conditions with his equipment always in superb shape and his rifle zeroed at the absolutely correct range. That's why the experienced hunter loves his sport so much. His skill is involved, his judgment is required, his intelligence is always called for - and he will face real challenges in the field. His need is to prepare for those challenges, both in his selection of equipment and his preparation for the field. Any hunter's odds are greatly improved when he chooses the right gun, the right bullet, and the right load for the task at hand. As much as a shooter needs to understand such variables as trajectories, the effects of wind drift, and bullet velocities over anticipated hunting ranges, so, too, must he give thought to the energy that the bullet will generate upon impact.
A bullet's kinetic energy, measured in foot-pounds, is a proxy for what's generally termed "stopping power." It has been assumed, the higher a bullet's energy at the point of impact, the greater its "stopping power." There are some caveats here. A bullet completely releases its energy in the target only if it remains in the game animal. If it has more than the adequate energy it may do its job and exit. This is certainly no cause for alarm. If it does not have sufficient energy to bring about a kill, whether through improper bullet choice or shots at excessive ranges, that is a cause for alarm. Responsible hunters make sure they can get the job done with the tools they have chosen. Taking shots at ranges where a bullet cannot reliably hit and kill a game animal is quite irresponsible behavior.
Hornady bullets for varminting are designed to fly fast and to release their high kinetic energy instantaneously and explosively. Should they be too powerful for a particular varmint and pass on through, the wound channel and exit hole will attest to their destructive power.
Hornady bullets for game hunting are designed for reliable, controlled expansion in all hunting bullet designs. No hunting bullet can be as effective as possible if it does not expand to a larger diameter than its caliber dimension. Expansion slows the bullet and allows it to shed kinetic energy as it does. All Hornady Bullets for hunting are made with the InterLock or InterBond features that bind jacket and core. This assures a heavier mass to penetrate the game animal and propagate shock waves within it. The higher the terminal velocity of the bullet, the higher its terminal energy. Expansion and penetration ensure energy release which in turn produces lethal results - and more certain kills.
This is not, nor is it intended to be, the final word on hunting bullet performance. Rather, we hope to stimulate your thinking about the subject and how important terminal bullet energies are to performance. Terminal energies and superior bullet expansion design permit the complete release of a bullet's remaining energy within the game animal. Hornady Bullets are backed by over 60 years of expertise on the subject.